 Advent of Code 2017, Day 11: Hex Ed
Advent of Code 2017, Day 11: Hex Ed
Day 11: Hex Ed
A very witty title for today’s challenge. It’s all about hexagons, and navigating a grid of them. Hexagonal grids cannot easily be mapped to x-y coordinates, however there is a fantastic resource all about hexagons by Amit Patel.
In order to tackle today’s challenge, we will lean heavily on the section named Cube Coordinates, so go read that now.
Our hexagons are arranged in a ‘flat-topped’ format, so be sure to switch the examples on that page to flat-topped so that they make sense.
The hexagons (“hexes”) in this grid are aligned such that adjacent hexes can be found to the north, northeast, southeast, south, southwest, and northwest
An ASCII representation of our flat-topped hexagon grid is provided on our challenge text page.
\ n /
nw +--+ ne
/ \
-+ +-
\ /
sw +--+ se
/ s \
As you can see from the example, we can go north, northeast, southeast, south, southwest, or northwest. The directions are shortened to n, ne, se, s, sw, and nw - but we need a way of representing our position in this infinite hexagon grid, and a way to update our position when we move in one of these directions.
After reading through the blog post you should come across this rather helpful picture which shows how we can represent our position using three dimensions, x, y and z.
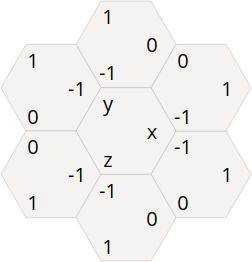
Whenever we move in a particular direction, we need to update the values of two of our dimensions.
For example, if we move northeast (ne), we need to add 1 to our x, 0 to our y, and -1 to our z (thus y stays the same). If we were moving south, we need to add 0 to our x, -1 to our y and 1 to our z.
We can represent our position, x y z, as a list of 3 numbers, with the origin being 0 0 0.
As we’ve just seen, if we move ne we should add 1 0 -1 to our position, if we move s we should add 0 -1 1 to our position. The mappings are as follows:
dir| x y z
---| --------
n | 0 1 -1
ne | 1 0 -1
se | 1 -1 0
s | 0 -1 1
sw | -1 0 1
nw | -1 1 0
Now we have a mapping listed for each of the 6 directions, let’s fire up a Q session and get to work.
Solving Part 1
We have come across the Q dictionary data type in earlier challenges, but this is the first time we need to construct a full one from scratch.
Dictionary creation is done with the ! operator, the left argument is a list of keys, the right argument is the list of values. If we try to build a dictionary with an differing count of keys and values we will get a 'length error.
We can use any type as the key to a table (within reason), generally keys are of symbol type (in case we want to turn our dictionary into a table at some point):
q)show d:`a`b`c!1 2 3 / symbols as the key, longs as the values
a| 1
b| 2
c| 3
q)d[`b] / indexing into dictionary with key `b
2
q)d`c / indexing in with key `c
3
q)d`d / there is no `d in the dictionary, so we get a null of type of the first item
0N
… but we can use any combination of key and value types to create a dictionary if we want:
q)show d:"abcd"!1 2 3 4 / chars are the keys, longs are the values
a| 1
b| 2
c| 3
d| 4
q)d"ac" / we can index on multiple keys at the same time
1 3
q)show d:0 1 2 3!({x+1};{x+2};{x*3};{x-1}) / keys are longs, functions are the values!
0| {x+1}
1| {x+2}
2| {x*3}
3| {x-1}
q)d[2] 10 / index in with key 2 and then pass 10 to the function ({x*3})
30
We will come across more complex dictionary mappings in later challenges. For now we just need to map a list of symbols `n`ne`se`s`sw`nw to list of lists of longs.
We can either do this step-by-step from an empty dictionary:
q)d:()!() / initialise an empty dictionary
q)d[`n]:0 1 -1
q)d[`ne]:1 0 -1
q)d[`se]:1 -1 0
q)d[`s]:0 -1 1
q)d[`sw]:-1 0 1
q)d[`nw]:-1 1 0
q)d / check our dictionary look ok
n | 0 1 -1
ne| 1 0 -1
se| 1 -1 0
s | 0 -1 1
sw| -1 0 1
nw| -1 1 0
… or if you are feeling brave, and don’t usually make typos you can create it as a one-liner:
q)d:`n`ne`se`s`sw`nw!(0 1 -1;1 0 -1;1 -1 0;0 -1 1;-1 0 1;-1 1 0)
q)d / check our dictionary look ok
n | 0 1 -1
ne| 1 0 -1
se| 1 -1 0
s | 0 -1 1
sw| -1 0 1
nw| -1 1 0
The first example states that if we head ne,ne,ne we will end up 3 steps away:
q)d`ne`ne`ne
1 0 -1
1 0 -1
1 0 -1
In order to find our our distance from the origin, we need to sum these up, and take the greatest absolute value using max:
q)sum d`ne`ne`ne / this is our position after all steps have been taken
3 0 -3
q)abs sum d`ne`ne`ne / abs will give us the absolute distance in any direction
3 0 3
q)max abs sum d`ne`ne`ne / and max will give us the largest distance from origin
3
To show that this wasn’t just a fluke, let’s try on the next example. ne,ne,sw,sw should return us to the origin:
q)sum d`ne`ne`sw`sw / the ne and sw movements have cancelled each other out
0 0 0
q)abs sum d`ne`ne`sw`sw / abs of zero is still zero
0 0 0
q)max abs sum d`ne`ne`sw`sw / max of a list of zeros is zero!
0
Now for the last two examples:
q)max abs sum d`ne`ne`s`s / ne,ne,s,s is 2 steps away
2
q)max abs sum d`se`sw`se`sw`sw / se,sw,se,sw,sw is 3 steps away
3
Looks good. Now let’s read in our puzzle input and feed that into our dictionary.
q)read0 `:input/11.txt
"s,se,ne,ne,ne,ne,ne,ne,ne,n,sw,sw,nw,sw,n,nw,nw,sw,nw,nw,nw,nw,sw,nw,nw,nw,nw,s,nw,nw,sw,nw,sw,sw,sw,nw,sw,sw,sw,sw,sw,sw,sw,s,sw,sw,sw,sw,se,sw,s,s,sw,s,ne,nw,nw,s,n,s,sw,s,sw,nw,se,s,s,s,s,s,nw,s,nw,s,s,se,se,se,se,se,se,s,se,s,s,se,n..
A comma-separated list of directions. We will take the first line, use vs to split on "," like we did in Day 10, but instead of casting to longs with the big-J casting, we will cast to symbol using `$
q)`$ "," vs first read0 `:input/11.txt
`s`se`ne`ne`ne`ne`ne`ne`ne`n`sw`sw`nw`sw`n`nw`nw`sw`nw`nw`nw`nw`sw`nw`nw`nw`nw`s`nw`nw`sw`nw`sw`sw`sw`nw`sw`sw`sw`sw`sw`sw`sw`s`sw`sw`sw`sw`se`sw`s`s`sw`s`ne`nw`nw`s`n`s`sw`s`sw`nw`se`s`s`s`s`s`nw`s`nw`s`s`se`se`se`se`se`se`s`se`s`s`se`n..
If we feed this directly into our dictionary, d, then apply max abs sum we will unlock today’s first star!
q)max abs sum d`$ "," vs first read0 `:input/11.txt
761
Solving Part 2
How many steps away is the furthest he ever got from his starting position?
We cannot use sum as this gives us the result after all of the steps are taken. In the same way that scan is the sister function to over (printing out results of each step), sums is the sister function to sum which will return each intermediate step:
q)sum til 10
45
q)sums til 10
0 1 3 6 10 15 21 28 36 45
This is because sum is addition over a list, and sums is addition scan a list:
q)(+) over til 10
45
q)(+) scan til 10
0 1 3 6 10 15 21 28 36 45
Or, if we wanted to get a little more hardcore, we could drop the syntactic sugar that Q adds, and use the raw K functions:
q)k)+/!10 / ! is 'til', '/' is over
45
q)k)+\!10 / '\' is scan
0 1 3 6 10 15 21 28 36 45
OK, so we want to use sums to get us the distance from origin for each step along the route.
q)sums d`$ "," vs first read0 `:input/11.txt
0 -1 1
1 -2 1
2 -2 0
3 -2 -1
4 -2 -2
5 -2 -3
..
Again, we can use abs to get absolute values:
q)abs sums d`$ "," vs first read0 `:input/11.txt
0 1 1
1 2 1
2 2 0
3 2 1
4 2 2
5 2 3
If we apply max we get the maximum direction in each of the x, y, or z dimensions.
q)max abs sums d`$ "," vs first read0 `:input/11.txt
1542 872 1145
… we can take the max again, and this will give us our second star!
q)max max abs sums d`$ "," vs first read0 `:input/11.txt
1542
Complete Solution To Day 11
My full solution for Day 11 is below. Note that I use sums for Part 1, and simply take the last value (which would be the result of performing sum). For Part 2 it is slightly quicker on my machine to flip the result of sums before performing the abs and max operations:
q)\t:1000 max max abs sums d`$ "," vs first read0 `:input/11.txt / perform the step 1000 times
2097
q)\t:1000 max max abs flip sums d`$ "," vs first read0 `:input/11.txt / around 30% faster
1390